von Dr. Julia Sudhoff Santos (Gewinnerin Dissertationspreis 2023)
Ordinale Kosten werden verwendet, wenn eine Größe nicht numerisch messbar ist, sondern sich nur in geordnete Kategorien (zum Beispiel gut, mittel, schlecht) einordnen lässt. Bekannte Skalen dieser Art sind der Nutri-Score auf Lebensmitteln, die Stufe der Tierhaltungsform bei Fleisch, oder olympische Medaillen. Es gibt verschiedene Möglichkeiten die Länder bei Olympia zu ranken, weil nicht klar ist um wie viel besser Gold- verglichen mit Silber- und Bronzemedaillen sind. So gibt es verschiedene Ansätze, wie zum Beispiel die Länder nach der Gesamtzahl der Medaillen oder lexikographisch zu sortieren. Dies verdeutlicht, dass Optimierungsprobleme mit ordinalen Kosten mehrere optimale Lösungen haben können, welche nicht miteinander vergleichbar sind.
Diese Eigenschaft teilen sie mit den vielfach untersuchten multikriteriellen Optimierungsproblemen. Diese Ähnlichkeit hat eine mathematische Erklärung: Optimierungsprobleme mit ordinalen Kosten können durch eine lineare Transformation in äquivalente multikriterielle Optimierungsprobleme umgeformt werden, wobei die Problemstruktur erhalten bleibt und nur die Zielfunktion angepasst wird.
Um dieses Vorgehen zu erklären, betrachten wir ein kleines Beispiel, welches in Abbildung 1 visualisiert wird. Wir nehmen an, dass der Graph die Straßen einer Stadt modelliert. Alle Straßen sind gleich lang und sie sind bezüglich ihrer Sicherheit für Radfahrer in eine von drei Kategorien eingeteilt. Grün (Kategorie 1) sind alle Wege mit separatem Radweg ohne Autoverkehr, orange (Kategorie 2) sind die Straßen mit aufgemaltem Radweg auf der Straße und rot (Kategorie 3) sind die Straßen ohne Radweg. Gesucht sind sichere Radwege von s nach t. Alle kreisfreien Wege sind in Abbildung 1 zusehen und mit P1 bis P4 bezeichnet. Offensichtlich ist der Weg P1 besser als der Weg P2, weil der Weg P2 zusätzlich zwei orange Kanten enthält. Analog ist auch Weg P4 besser als Weg P3, weil er zwei grüne statt zwei orangen Kanten nutzt. Die Wege P1 und P4 sind hingegen nicht vergleichbar, da unklar ist ob eine rote Kante oder eine grüne und zwei orange Kanten bevorzugt werden. Daher sind die beiden Wege P1 und P4 die relevanten, d.h., ordinal nicht-dominierten Lösungsalternativen für dieses Problem.
Für jeden der Wege P1 bis P4 gibt der in Abbildung 1 angegebene Vektor c in der i-ten Komponente an, wie viele Wegabschnitte in Kategorie i eingeordnet sind für i=1,2,3. Mit Hilfe dieser Vektoren können zwei Lösungen verglichen werden, indem man die Summen über die letzten Einträge der Vektoren vergleicht. Formal sagen wir ein Weg P* dominiert einen Weg P‘, wenn
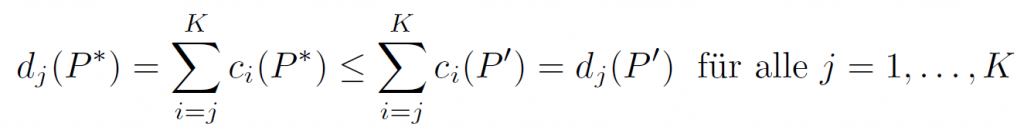
und c(P*) ungleich c(P‘) ist. Um diesen Vergleich leichter durchführen zu können, definieren wir die Vektoren d, welche in der i-ten Komponente zählen, wie viele Elemente in Kategorie i oder schlechter sind. Diese Vektoren lassen sich dann komponentenweise bezüglich der Pareto-Dominanz vergleichen. Der komponentenweise Vergleich führt wie erwartet dazu, dass die Vektoren d(P1) und d(P4) sich gegenseitig nicht dominieren, während d(P1) den Vektor d(P2) und d(P4) den Vektor d(P3) dominiert.
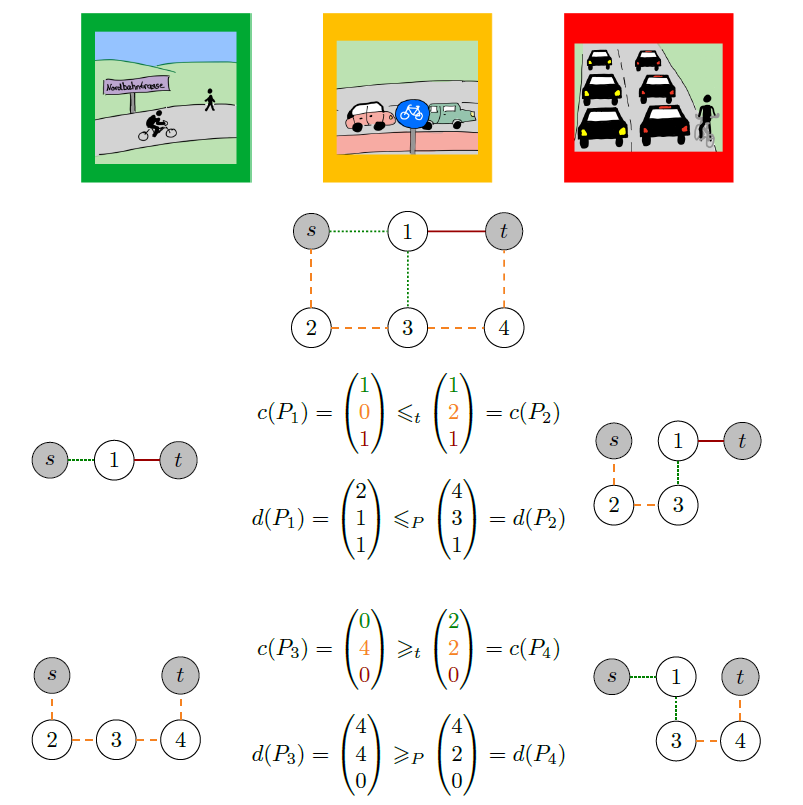
Abbildung 1: Beispielproblem zur Berechnung sicherer Radwege von s nach t.
Wenn die ordinalen Kosten über den Vektor d bezüglich Pareto-Dominanz verglichen werden, erhalten wir ein äquivlantes multikriterielles Optimierungsproblem mit unveränderter zulässiger Menge. Daher können problemspezifische multikriterielle Lösungsalgorithmen verwendet werden. Diese Lösungsansätze können analog auch auf Probleme mit Kombinationen von ordinalen Kosten mit zusätzlichen reellen Zielfunktionen angewandt werden.
In [1] haben wir die oben beschriebenen Möglichkeiten und eine weitere Variante der Modellierung ordinaler Kosten in kombinatorischen Optimierungsproblemen beschrieben und untersucht. Insbesondere haben wir auch den ordinalen Ordnungskegel auf den Vektoren c mit dem Ordnungskegel der Pareto-Dominanz verglichen, welcher auf den Vektoren d angewendet wird. Der ordinale Ordnungskegel und der Pareto-Kegel sind in Abbildung 2 in drei Dimensionen visualisiert.
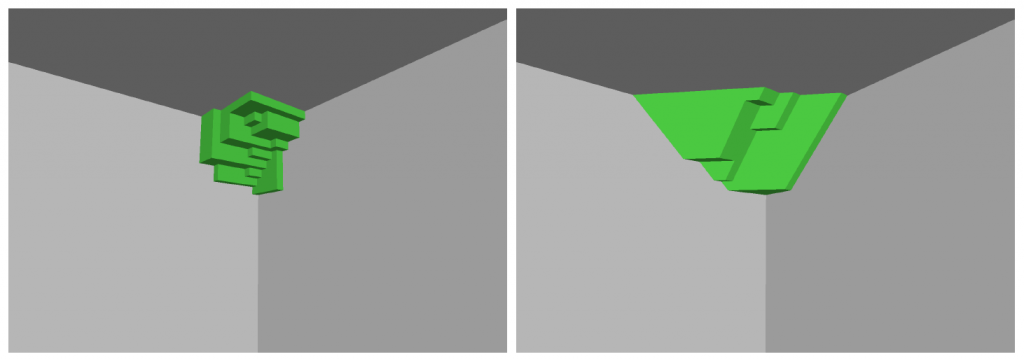
Abbildung 2: Das linke Bild zeigt eine nicht-dominierte Menge und den von dieser Menge dominierten Bereich bezüglich der Pareto-Dominanz in grün. Das rechte Bild zeigt von dieser Menge noch die Punkte, die bezüglich der ordinalen Dominanz nicht dominiert sind, und den von ihnen dominierten Bereich in grün.
In meiner Thesis [2] werden ordinale Kosten auch im spezifischeren Kontext der Matroidoptimierungsprobleme untersucht. In diesem Spezialfall kann das Problem mit nur einer ordinalen Zielfunktion mit Hilfe des Greedy Algorithmus gelöst werden, da ordinale Kosten sortierbar sind, siehe [3]. Darüber hinaus haben wir in [3] einen polynomiellen Lösungsalgorithmus entwickelt, um Matroidprobleme mit einer reellen und einer ordinalen Zielfunktion zu lösen. Nimmt man an, dass die ordinale Zielfunktion nur aus zwei Kategorien besteht, so ist dieses bei Matroidproblemen äquivalent zu einer binären Zielfunktion. In [4] haben wir einen Lösungsalgorithmus vorgestellt, welcher ein Matroidproblem mit einer reellen und einer binären Zielfunktion in einer linearen Anzahl an Iterationen (bezüglich der Anzahl der nicht-dominierten Lösungen) lösen kann. Des weiteren haben wir gezeigt, dass die Menge der effizienten Lösungen in diesem Fall bezüglich einer einfachen Nachbarschaftsdefinition zusammenhängend ist. Insgesamt liefert die Thesis [2] viele Beiträge für ein tieferes Verständnis über die Modellierung ordinaler Kosten und das Lösen ordinaler Optimierungsprobleme.
Literaturverzeichnis
- Klamroth, K., M. Stiglmayr, and J. Sudhoff (2022). „Ordinal Optimization Through Multiobjective Reformulation“. In: European Journal of Operational Research, Volume 311, Issue 2, 2023, Pages 427-443, doi: 10.1016/j.ejor.2023.04.042.
- J. Sudhoff (2022). „Ordinal Costs in Multi-objective Combinatorial Optimization“. University of Wuppertal, PhD Thesis
- Klamroth, K., M. Stiglmayr, and J. Sudhoff (2022). “Multi-objective Matroid Optimization with Ordinal Weights”. In: Discrete Applied Mathematics, Volume 335, 2023, Pages 104-119, doi: 10.1016/j.dam.2022.07.017.
- Gorski, J., K. Klamroth, and J. Sudhoff (2022). “Biobjective optimization problems on matroids with binary costs”. In: Optimization, Volume 72, Issue 7, 2023, Pages 1931-1960, doi: 10.1080/02331934.2022.2044479.
