Multidimensionale Optimierung und das Problem der k kürzesten Wege

von Max Huneshagen (Gewinner Masterpreis 2023)

Viele Millionen Menschen fliegen jedes Jahr von Deutschland aus zu Zielen in Nah und Fern. Nur die Wenigsten werden sich dabei fragen, welchen Weg sie eigentlich genau nehmen. Aus der Sicht von Fluggesellschaften kann sich die Wahl der optimalen Flugroute als ein kompliziertes Problem herausstellen. Auf den ersten Blick könnte man meinen, dass man immer den direkten Weg wählen sollte – schließlich ist dieser am kürzesten und daher doch wohl sicher auch am billigsten? In der Realität ist dieser naive Ansatz leider zumeist falsch, da weitere Kosten berücksichtigt werden müssen, die nicht unbedingt proportional mit der Weglänge steigen. So verlangen beispielsweise Staaten Gebühren für das Überqueren ihres Hoheitsgebietes. Deswegen kann es womöglich günstiger sein, eine längere Strecke über ein Land mit geringen Gebühren zu fliegen als nur kurz über ein Land, das viel Geld für einen Überflug verlangt. Außerdem spielen die Stärke und Richtung des Windes eine wichtige Rolle in der Flugplanung, was dazu führt, dass Flugrouten oft dynamisch geplant werden müssen.

Optimalität bei mehrdimensionalen Kosten

Mathematiker sprechen bei Problemen dieser Art von multidimensionaler Optimierung. Anders als bei klassischen Optimierungsproblemen, bei denen eine Lösung x aus einem Lösungsraum L gesucht wird, sodass die Kosten c(x)∈ ℝ minimal werden, hat man es hier mit mehreren Kostenfunktionen gleichzeitig zu tun, oder dem sogenannten „Kostenvektor“ c(x)∈ ℝ^d. Doch welche Bedingungen sollte x erfüllen, um optimal zu sein? Diese Frage stellt sich, da man nicht alle mehrdimensionalen Vektoren ohne weiteres vergleichen kann. Ohne Zweifel sind die Kosten (2, 4) den Kosten (3,5) vorzuziehen, aber wie sollte man beispielsweise mit (2,5) und (3,4) umgehen, welchen Kostenvektor sollte man bevorzugen?

Diese Frage beantwortet der Begriff der Dominanz. Wir sagen dass ein Kostenvektor v¹ den Kostenvektor v² dominiert, wenn v¹ in allen Komponenten kleiner ist als v² und strikt kleiner in mindestens einer Komponente. Wenn es in einer Menge C von Kostenvektoren keinen gibt, der x ∈ C dominiert, so nennen wir x nicht-dominiert in C. Wählen wir nun als C die Menge aller Kosten der Elemente in unserer Lösungsmenge L, C=c(L), dann erhalten wir (unter bestimmten technischen Bedingungen, auf die wir an dieser Stelle nicht näher eingehen wollen) eine Menge von Elementen in C, deren Kosten nicht-dominiert sind. Diese so genannten effizienten Elemente sind genau diejenigen, an denen die multidimensionale Optimierung interessiert ist.

In Bezug auf die Frage von oben bedeutet dies, dass man weder den Vektor (2, 4) noch den Vektor (3,5) gegenüber dem anderen bevorzugt, sondern beide in der Menge der nicht-dominierten Kosten sein können, wenn sie von keinem anderen Vektor dominiert werden. Es ergibt also in mehreren Dimensionen im Allgemeinen wenig Sinn, nach den einen optimalen Kosten zu fragen, denn in der Regel wird es mehrere effiziente Kostenvektoren geben. Nicht nur aus diesem Grund ist es oft sinnvoll, die Suche nach effizienten Routen nicht auf der riesigen Menge aller theoretisch vorstellbaren Wege durchzuführen, sondern sich auf ein Raster zu beschränken. Solche Wege beschreiben einen Graphen mit n Knoten und m Kanten. Das Problem, effiziente Wege (ohne Schleifen) einem solchen Graphen zu finden, bezeichnet man als multiobjektives kürzeste-Wege-Problem (engl. multiobjective shortest paths problem, MOSP). Maristany et al. [] stellten einen Algorithmus vor, den sie MDA (engl. multidimensional Dijkstra algorithm) nannten und der dieses Problem effizient löst, und zwar in einer Laufzeit von O(dN_max(nlog(n)+N_maxm)). N_max ist dabei die maximale Anzahl von effizienten Pfaden vom Startknoten zu einem beliebigen anderen Knoten. Eine solche Laufzeit wird als output-sensitiv bezeichnet, weil die Größe des Outputs (also die Anzahl der effizienten Pfade) die Laufzeit beeinflusst.

Lösen des Problems der k kürzesten Wege mit multidimensionaler Optimierung

Die Motivation meiner Masterarbeit war es, diesen Algorithmus auf ein anderes verwandtes Problem anzuwenden. Kehren wir dazu zunächst zu eindimensionalen Kosten zurück. Ein Netzwerk, dessen Kosten in erster Näherung vereinfachend als eindimensional angenommen werden können, ist das Gleisnetz. Will man von A nach B gelangen, so ist es oft hilfreich, die ersten paar schnellsten Anbindungen zu betrachten und diese händisch zu vergleichen, um so beispielsweise eine Route zu wählen, die man schon aus vorherigen Reisen kennt oder die die schönste Landschaft durchquert. Die meisten Routenplaner geben hierzu nicht nur den kürzesten, sondern auch den zweit- und eventuell den drittkürzesten Weg an (s. Abb. 1). Es gibt zahlreiche weitere Anwendungen, für die man mehr als nur den erstkürzesten Weg wissen möchte.

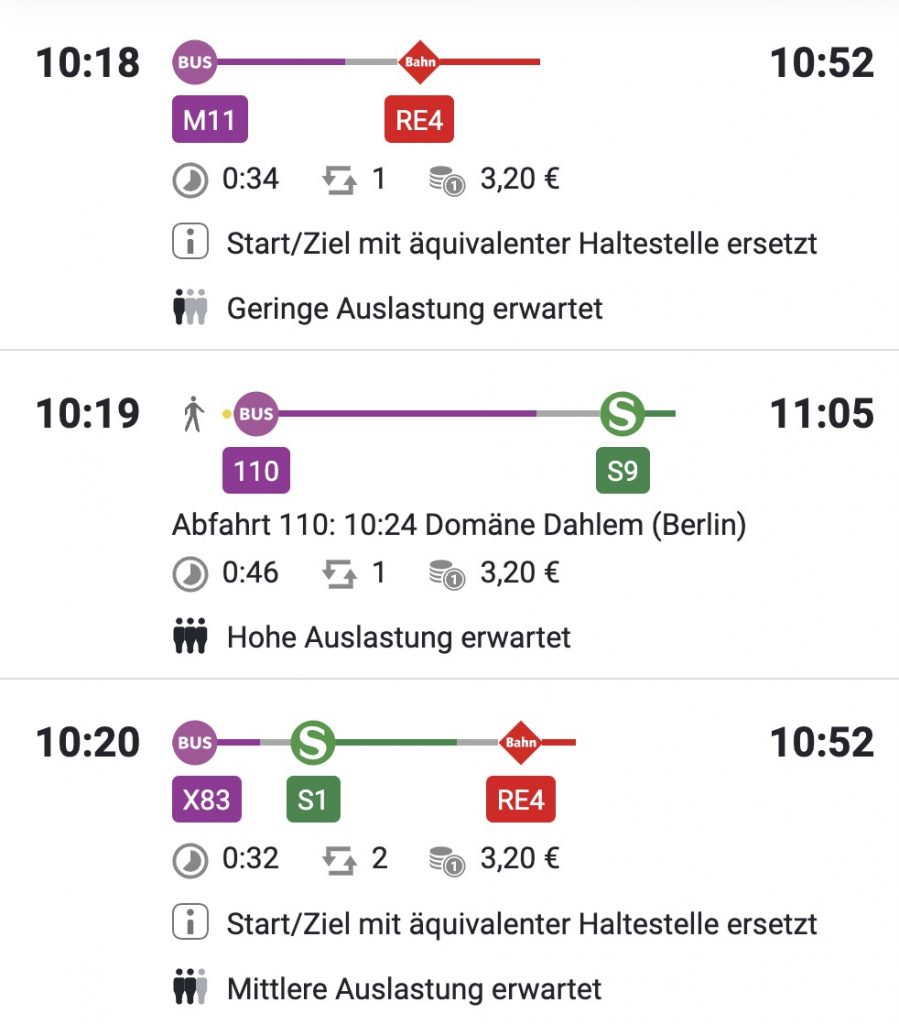
Abb. 1: Die App der Berliner Verkehrsbetriebe erlaubt dem User, mehrere kurze Wege zu betrachten und einen auszuwählen (Quelle: bvg.de).

Man sucht hierfür also im Allgemeinen nach den k kürzesten Wegen zwischen A und B für eine beliebige positive ganze Zahl k. Ein klassischer Algorithmus für dieses Problem ist der Algorithmus von Yen [], der den kürzesten Pfad P₁ mit Hilfe des Dijkstra-Algorithmus berechnet und dann k-1 Iterationen des gleichen Typs durchführt. In jeder dieser Iterationen durchschreitet der Algorithmus die Knoten des zuletzt gefundenen Pfades und sucht nach kürzesten Alternativen von diesem Knoten aus. Die so gefundenen Pfade werden in einem Heap gespeichert und am Ende jeder Iteration wird der kürzeste Pfad als nächstkürzester Pfad von A nach B ausgegeben. Damit man nicht manche Pfade doppelt findet, müssen für jeden Knoten verschiedene Kanten des Graphen gelöscht und später wieder hinzugefügt werden. Diese Vorgehensweise speichert oft unnötig viele relativ lange Wege und ist in der Praxis oft langsam, wenngleich die theoretische Komplexität lange Zeit als optimal galt, bevor sie 2009 von Gotthilf und Lewenstein [] unterboten wurde. Da letzterer jedoch schwer zu implementieren ist und vermutlich für Graphen von heute zugänglicher Größe keine Besserung bringen würde, wird der Algorithmus von Yen weiterhin als wichtiger Benchmark-Algorithmus benutzt.

Ein anderer Ansatz für das Problem der kürzesten Wege geht auf eine Arbeit von Roddity und Zwick [] zurück. Diese organisierten die ersten l<k kürzesten Wege in einer Baumstruktur, dem sogenannten Abweichungsbaum. Vereinfachend erlaubt dieser die Klärung der Frage, ob der drittkürzeste Pfad der zweitkürzeste Umweg des kürzesten Pfades oder der kürzeste Umweg des zweitkürzesten Pfades ist. Präziser erlaubt der Abweichungsbaum eine Zuordnung eines Elternpfads zu jedem neu gefundenen Pfad. Die Idee von Roddity und Zwick ist es, nach dem kürzesten Pfad den zweitkürzesten Pfad als Kind des kürzesten zu berechnen und in ein Heap Q einzufügen. In der i-ten der k-1 Iterationen des Algorithmus wird nun der i-te kürzeste Pfad P_i aus Q extrahiert und anschließend das kürzeste Kind von P_i sowie das kürzeste noch nicht entdeckte Kind des Elternpfades von P_i berechnet. Somit wird die Berechnung der k kürzesten Pfade auf 2k solcher „kürzestes Kind“-Berechnungen zurückgeführt, die der Bestimmungen eines zweitkürzesten Weges entsprechen.

Ergebnisse

Die Idee in meiner Masterarbeit war es nun, für diese Berechnungen den Algorithmus von Maristany et al. zu verwenden. Dazu definierten wir eine zweite Kostenfunktion c₂, sodass der zweitkürzeste Pfad ein effizienter Pfad bezüglich des Kostenvektors (c₁,c₂) ist. Es stellt sich heraus, dass man hierfür genau die charakteristische Funktion des kürzesten Pfades wählen kann, c₂(P) zählt also, wie viele Kanten Pmit dem kürzesten Pfad gemeinsam hat. Mit dieser Kostenstruktur lässt sich der MDA als Subroutine im Algorithmus von Roddity und Zwick anwenden. Heraus kommt ein Algorithmus, der zwar die gleiche theoretische Komplexität wie der Algorithmus von Yen hat, in der Praxis aber für viele Graphen oft erheblich schneller ist, wie man in Abb. 2 am Beispiel des Straßennetzes von New York sehen kann. Eine Erklärung dieses Performance-Vorteils unseres neuen Algorithmus findet sich zu einem wesentlichen Teil darin, dass kurze Umwege schneller gefunden werden und weniger lange Pfade gespeichert werden müssen. Dies lässt sich quantifizieren, indem man die Heap-Operationen N zählt, die beide Algorithmen ausführen. Die Ergebnisse sind in Abb. 3 für den genannten Graphen zu sehen und zeigen, dass der neue Algorithmus in diesem Fall viel weniger Pfade speichern musste, was tatsächlich für viele verwendete Straßennetzwerke und Gittergraphen zutrifft. In meiner Arbeit wird jedoch gezeigt, dass dies keineswegs immer der Fall ist und der neue Algorithmus bei bestimmten Graphen mehr Pfade in den Heap einfügen muss. Bei diesen „schlechten” Graphen handelt es sich allerdings um sorgfältig konstruierte Beispiele, die in der Praxis nicht relevant sind.

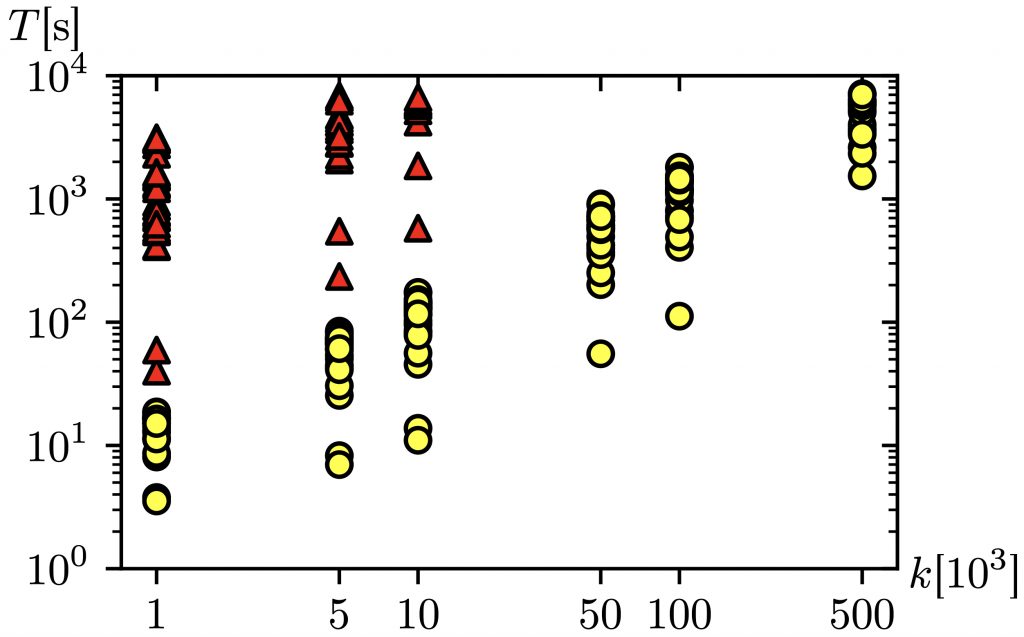
Abb. 2: Zeit die der Algorithmus von Yen (rot) und der neue Algorithmus (gelb) benötigen, um k kürzeste Wege zu berechnen. Für jedes k wurden 30 verschiedene Start- und Endpunkte zufällig gewählt.

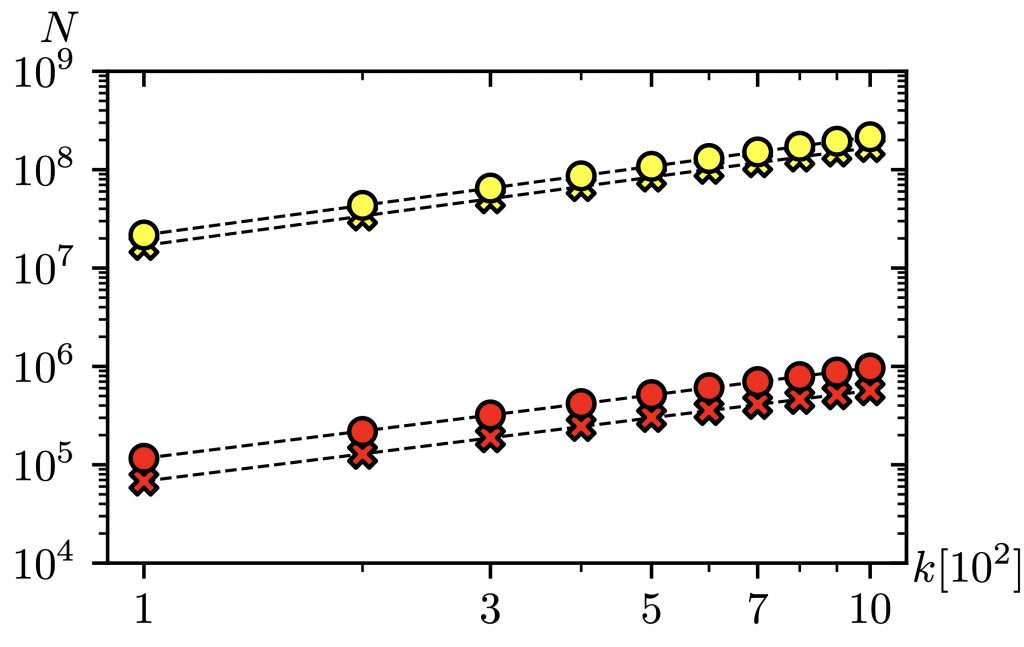
Abb. 3: Anzahl der benötigten Heap-Einsetzungen (Kreise) und Heap-Extraktionen (Kreuze) für den Algorithmus von Yen (gelb) und den neuen Algorithmus (rot) im Falle des Straßennetzes von New York mit zufällig gewählten Start- und Endknoten für verschiedene k. Die Anstiege sind beide in etwa linear, N~k¹.

Literatur

1. Maristany de las Casas, P., Sedeño-Noda, A., und Borndörfer, R.: An Improved Multi- objective Shortest Path Algorithm. In: Comput. Oper. Res. 135 (2021), p. 105424.
2. Yen, J. Y.: An algorithm for finding shortest routes from all source nodes to a given destination in general networks. In: Q. Appl. Math. 27.4 (1970), pp. 526–530.
3. Gotthilf, Z. und Lewenstein, M.: Improved algorithms for the 𝑘 simple shortest paths and the replacement paths problems. In: Inf. Process. Lett. 109.7 (2009), pp. 352–355.
4. Roditty, L. und Zwick, U.: Replacement Paths and 𝑘 Simple Shortest Paths in Un- weighted Directed Graphs. In: ACM Trans. Algorithms 8.4 (2012).