von Nils Mosis (Gewinner Masterpreis 2023)
Simplex Algorithmus
Der Simplex Algorithmus wurde 1947 von George Dantzig entwickelt [1] und wird bis heute für die Lösung linearer Optimierungsprobleme genutzt. Der Algorithmus startet in einer Ecke der zulässigen Menge und bewegt sich dann iterativ zu benachbarten Ecken mit einem verbesserten Zielfunktionswert, bis er eine optimale Lösung findet (siehe Abb. 1) oder erkennt, dass das lineare Programm (LP) unbeschränkt ist.
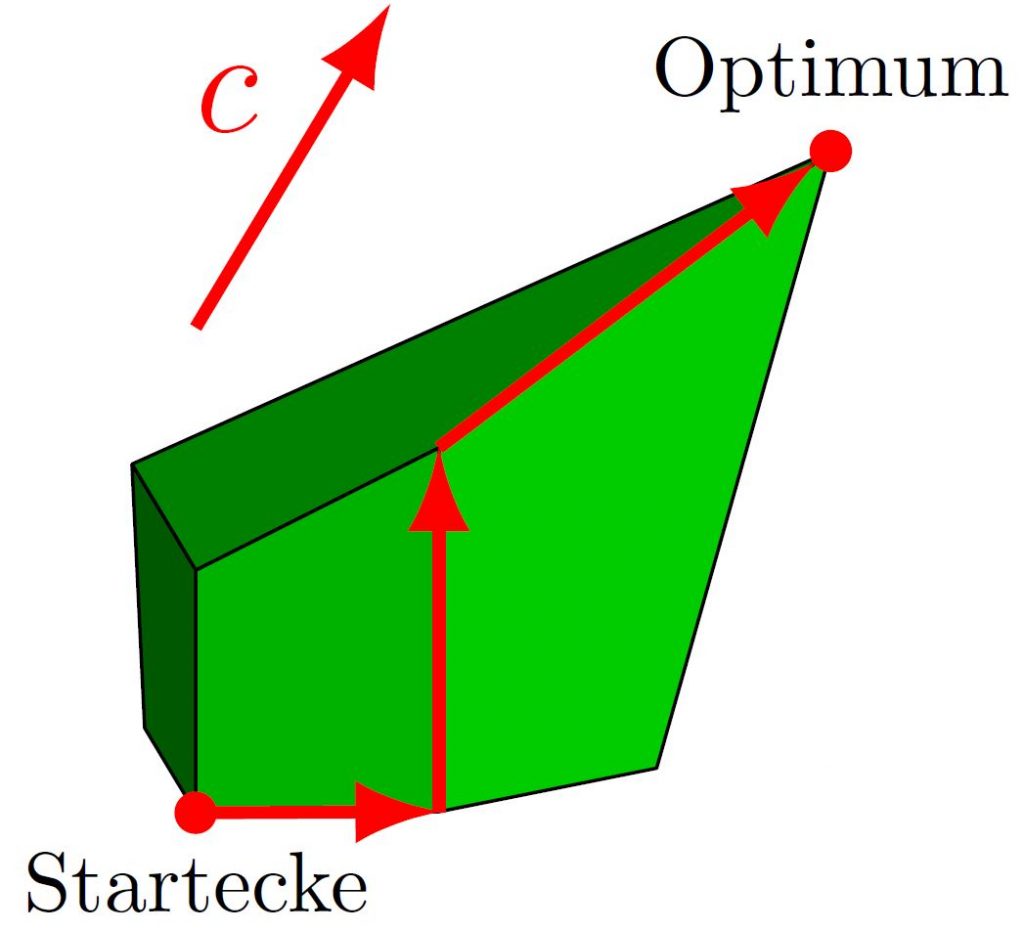
Abb. 1: Das zulässige Polyeder eines LPs mit zu maximierendem Zielfunktionsvektor c. Der Simplex Algorithmus findet das Optimum hier in drei Schritten.
Das Simplex Verfahren kann nicht nur zur Lösung von LPs genutzt werden, sondern wird in Verbindung mit Branch-and-Bound Methoden auch zur Lösung gemischt-ganzzahliger linearer Programme (MIPs) herangezogen, was ihm einen breiten Anwendungsbereich im Operations Research garantiert. Außerdem ist der Algorithmus in der Praxis sehr effizient, was es seinen Anwendern ermöglicht, Probleme mit einer Vielzahl von Variablen und Nebenbedingungen zu lösen.
Allerdings ist die Laufzeit des Simplex Algorithmus seit seiner Entwicklung vor über siebzig Jahren noch immer Gegenstand aktiver Forschung. Im Allgemeinen gibt es viele verschiedene mögliche Pfade von der Startecke zum Optimum. So hat zum Beispiel die Startecke in Abbildung 1 zwei verschiedene Nachbarn mit besserem Zielfunktionswert. Die Wahl der Nachbarecken wird mit Hilfe von Pivotregeln getroffen. Dadurch hängt die Laufzeit des Algorithmus, also die Anzahl der besuchten Ecken, stark von der gewählten Pivotregel ab.
Trotz der Effizienz des Verfahrens in der Praxis gibt es super-polynomielle untere Schranken an die worst-case Laufzeiten von allen verwendeten Pivotregeln. Diese Diskrepanz zwischen praktischer Effizienz und theoretischer Ineffizienz macht die Frage, ob es eine polynomielle Pivotregel gibt, zu einer der bekanntesten offenen Fragen der Mathematischen Optimierung.
Das Finden einer solchen Regel würde Smales neuntes offenes Problem für das 21. Jahrhundert [2] beantworten („Gibt es einen streng polynomiellen Algorithmus für LPs?“) und die Polynomiale Hirsch Vermutung [3] bestätigen („Der kombinatorische Durchmesser jedes Polytops ist durch ein Polynom in der Anzahl seiner Facetten beschränkt.“).
Die erste exponentielle untere Schranke für den Simplex Algorithmus wurde anhand des Klee-Minty-Würfels bewiesen. Dort wird ausgenutzt, dass Dantzigs originale Pivotregel jede Ecke eines geeignet verzerrten Hyperwürfels besucht, obwohl der anfängliche und der optimale Eckpunkt benachbart sind. Danach wurden ähnliche Konstruktionen für alle klassischen Pivotregeln entwickelt. Diese Konstruktionen wurden von Amenta und Ziegler im Jahre 1999 vereinheitlicht [4].
Die ersten super-polynomiellen unteren Schranken für randomisierte oder erfahrungsbasierte Pivotregeln wurden dann in den 2010er Jahren vorgeschlagen. Diese nutzen alle eine enge Verbindung zwischen dem Simplex Algorithmus und dem Policy-Iteration-Algorithmus für Markov-Entscheidungsprozesse (engl. Markov Decision Processes, kurz: MDPs) aus. Für eine Übersicht über diese Konstruktionen verweisen wir auf [5].
Markov-Entscheidungsprozesse
MDPs werden in der Wahrscheinlichkeits- und Entscheidungstheorie dazu verwendet, sequentielle Entscheidungsprobleme unter Unsicherheit zu modellieren. Sie sind von großer Bedeutung in verschiedenen Bereichen wie der Ressourcenallokation, der Steuerung von Prozessen in Produktion und Logistik sowie im maschinellen Lernen.
Aus mathematischer Sicht besteht ein MDP aus vier Hauptkomponenten: Zuständen, Aktionen, Übergangswahrscheinlichkeiten und Belohnungen bzw. Kosten.
Genauer gesagt modelliert ein MDP ein System, das sich in verschiedenen Zuständen befinden kann. Ein Zustand könnte zum Beispiel eine Liste der aktuellen Lagerbestände in verschiedenen Standorten sein. Nun gibt es in jedem Zustand verschiedene ausführbare Aktionen, die das System in einen neuen Zustand überführen. Zum Beispiel könnte sich das Unternehmen dazu entscheiden, Produkte von Standort A nach Standort B zu verschieben. Manche Aktionen überführen das System mit gewissen Übergangswahrscheinlichkeiten in unterschiedliche neue Zustände. Zum Beispiel könnten mit einer gewissen Wahrscheinlichkeit Produkte auf dem Weg von A nach B verloren gehen oder zerstört werden, wodurch die resultierenden Lagerbestände nicht mit Gewissheit vorhergesagt werden können. Zuletzt entstehen in unserem Beispiel durch das Verschieben der Produkte Kosten in Höhe eines festen Betrags C.
Wie in Abbildung 2 zu sehen ist, können wir MDPs als Digraphen darstellen. Die runden Knoten repräsentieren hier die Zustände, deren ausgehenden Kanten die Aktionen. Nach Aktionen, die in einen eckigen Knoten führen, befindet sich das System in einem der direkten Nachfolger-Zustände jenes Knotens. Die Wahrscheinlichkeiten für jeden dieser Nachfolger und die Belohnungen der Aktionen sind durch die Kantenbeschriftungen gegeben.
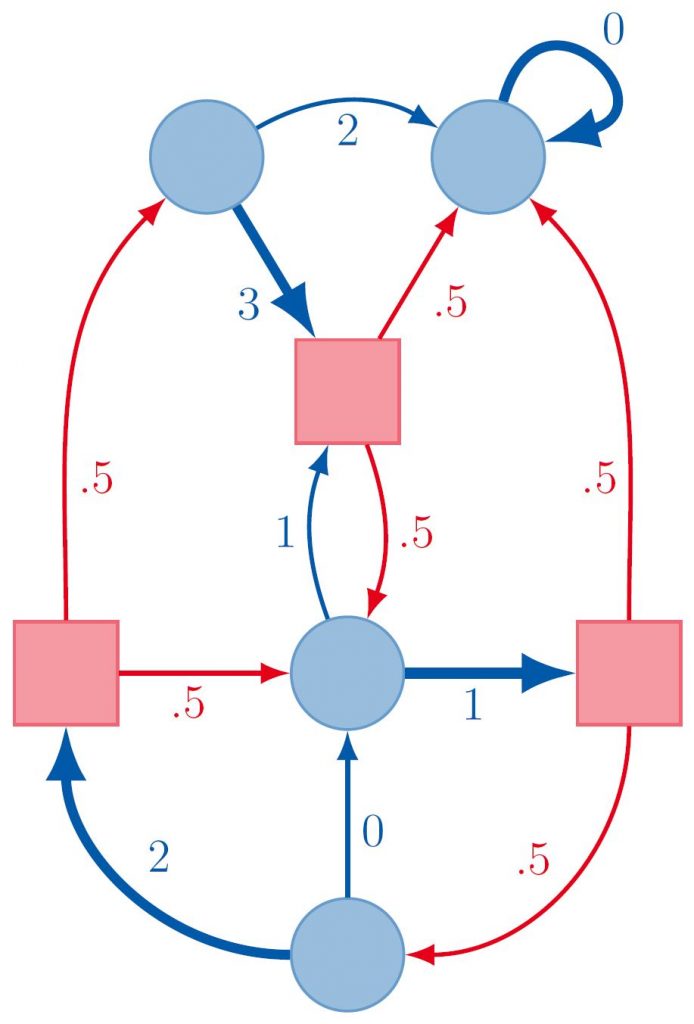
Abb. 2: Darstellung eines MDPs als Digraph. Die hervorgehobenen Kanten markieren die optimale Strategie.
Das Hauptziel in einem MDP besteht darin, eine Strategie (Policy) zu finden, die angibt, welche Aktion in jedem Zustand ausgewählt werden soll, um über die Zeit hinweg die maximale kumulative Belohnung zu erzielen bzw. die Kosten zu minimieren (siehe Abb. 2). Es gibt verschiedene Algorithmen, um eine optimale Strategie zu finden. Wir betrachten hier den Policy-Iteration-Algorithmus.
Der Algorithmus startet mit einer zulässigen Strategie für den MDP. Solange die aktuelle Strategie nicht optimal ist, verbessert er die Strategie, indem er die Wahl der Aktionen in einer Menge von ausgewählten Zuständen verändert. Wir betrachten hier die simple Variante des Policy-Iteration-Algorithmus, bei der in jeder Iteration die Strategie nur in genau einem Zustand verändert wird. Unter gewissen Voraussetzungen kann man zeigen, dass diese Methode immer zu einer optimalen Strategie führt. Wie beim Simplex Algorithmus wird die Wahl der verbessernden Aktion mit Hilfe von Pivotregeln getroffen.
Simplex Algorithmus und Policy-Iteration
Wir halten fest, dass sowohl der Simplex Algorithmus als auch der Policy-Iteration-Algorithmus mit einer zulässigen Lösung beginnen und Pivotregeln verwenden, um die lokalen Optimierungsrichtungen festzulegen, die sie am Ende zu einer optimalen Lösung führen.
Diese Ähnlichkeit lässt sich zu einer Transformation formalisieren, die besagt, dass sich gewisse MDPs in LPs von gleicher asymptotischer Größe umwandeln lassen, sodass der Simplex Algorithmus sich wie Policy-Iteration verhält [6]. Genauer gesagt gibt es eine Bijektion zwischen Strategien des MDPs und Eckpunkten des zulässigen Bereichs des LPs. Wählen wir analoge Pivotregeln für beide Algorithmen, dann ist die Abfolge der Strategien, die vom Policy-Iteration-Algorithmus besucht werden, dieselbe (im Hinblick auf die Bijektion) wie die Abfolge der Eckpunkte, die vom Simplex Algorithmus besucht werden.
Dieser Zusammenhang ermöglicht es uns, Laufzeitschranken für Simplex Pivotregeln anhand von MDPs zu beweisen: wir konstruieren eine Familie von MDPs, sodass Policy-Iteration eine große Anzahl an Iterationen ausführen muss; dann zeigen wir, dass diese MDPs die (üblicherweise leicht überprüfbaren) Voraussetzungen aus [6] erfüllen; bei analoger Wahl der Pivotregeln erhalten wir somit dieselbe untere Schranke für den Simplex Algorithmus.
Unsere Ergebnisse
Im Hauptresultat der Masterarbeit zeigen wir, dass jede (deterministische oder randomisierte) Kombination von Dantzigs Pivotregel, Blands Pivotregel und der sogenannten Largest-Increase-Regel eine exponentielle worst-case Laufzeit hat. Dies gilt für den Simplex Algorithmus sowie für den Policy-Iteration-Algorithmus.
Kombination verschiedener Regeln meint, dass wir diese während der Ausführung der Algorithmen wechseln dürfen – oder anders gesagt: die drei Regeln liefern uns in jeder Iteration (bis zu) drei verschiedene Kandidaten, also bessere Ecken bzw. Aktionen, von denen wir dann einen aussuchen können.
Eine Beschreibung der genannten Pivotregeln sowie individuelle exponentielle Schranken für den Simplex Algorithmus mit diesen Regeln finden sich auch bei Amenta und Ziegler [4].
Während eine exponentielle Schranke an Blands Regel für Policy-Iteration bekannt ist [7], scheinen Dantzigs Regel und die Largest-Increase-Regel für diesen Algorithmus noch nicht betrachtet worden zu sein. Das liegt unserem Verständnis nach vor allem daran, dass Policy-Iteration meistens in einer Version betrachtet wird, in der mehrere Aktionen in verschiedenen Zuständen gleichzeitig verändert werden.
Um unser Resultat zu erhalten, übernehmen wir die bewährte Vorgehensweise aus den oben erwähnten MDP-Konstruktionen für randomisierte Pivotregeln. Intuitiv gesprochen, modelliert unser MDP einen Binärzähler mit log(N) Bits und wir definieren für jede log(N)-Bit-Binärzahl eine sogenannte kanonische Strategie, die diese Zahl repräsentiert. Da mit log(N) Bits genau N unterschiedliche Zahlen dargestellt werden können, erhalten wir eine exponentielle Laufzeit, wenn wir zeigen können, dass Policy-Iteration alle kanonischen Strategien besucht. Dafür wählen wir als Startstrategie die kanonische Strategie für Null und zeigen induktiv, dass der Algorithmus die kanonische Strategie für X in die kanonische Strategie für X+1 umwandelt.
Für tiefere Einblicke in die hier beschriebenen Themen und Resultate verweisen wir gerne auf [8].
Ausblick
Da es super-polynomielle untere Schranken für alle herkömmlichen Pivotregeln gibt, wird ein Schwerpunkt zukünftiger Forschung darauf liegen, neue Pivotregeln einzuführen und zu untersuchen. Es könnte ein interessanter Ansatz sein, Ähnlichkeiten zwischen den verschiedenen MDP-Konstruktionen herauszuarbeiten. Einerseits könnte das dabei helfen, diese unteren Schranken zu verallgemeinern und zu erweitern, um einige – oder vielleicht sogar größere Klassen von – Pivotregeln auszuschließen. Andererseits könnten solche Erkenntnisse zu einer neuen Pivotregel führen, die die Fallstricke der bisherigen Konstruktionen überwindet, und dadurch ein neuer hoffnungsvoller Kandidat auf der Suche nach der polynomiellen Pivotregel wird.
Literatur
- George B. Dantzig. Maximization of a linear function of variables subject to linear inequalities. Activity analysis of production and allocation 13 (1951): 339-347.
- Steve Smale. Mathematical problems for the next century. Mathematical Intelligencer 20.2 (1998): 7-15.
- Francisco Santos. A counterexample to the Hirsch conjecture. Annals of mathematics (2012): 383-412.
- Nina Amenta und Günter M. Ziegler. Deformed products and maximal shadows of polytopes. Contemporary Mathematics, 223:57-90, 1999.
- Alexander V. Hopp. The Complexity of Zadeh’s Pivot Rule. Logos Verlag Berlin, 2020.
- Martin L. Puterman. Markov decision processes: discrete stochastic dynamic programming. John Wiley & Sons, 1994.
- Mary Melekopoglou und Anne Condon. On the complexity of the policy improvement algorithm for Markov decision processes. ORSA Journal on Computing, 6(2):188-192, 1994.
- Yann Disser und Nils Mosis. (im Druck). A unified worst case for classical simplex and policy iteration pivot rules. The 34th International Symposium on Algorithms and Computation (ISAAC 2023).
