von Dr. Yasmine Beck (Gewinnerin des GOR Dissertationspreises 2025)
Optimierungsmodelle sind ein zentrales Werkzeug zur Unterstützung von Entscheidungsträgern in komplexen Entscheidungsprozessen. In der klassischen, einstufigen Optimierung wird angenommen, dass eine einzige Person oder Instanz alle Entscheidungen trifft – ein geeigneter Rahmen für viele Anwendungen in der Praxis, aber eben nicht für alle. In zahlreichen realen Situationen treffen mehrere Akteure Entscheidungen, die sich gegenseitig beeinflussen können. Ein Entscheidungsträger muss dabei oft antizipieren, wie andere auf seine Wahl reagieren werden. Zum Beispiel legt ein Unternehmen Preise für Waren oder Dienstleistungen fest, welche die Nachfrage der Kunden beeinflussen können. Im Verkehrsmanagement bestimmen Behörden Mautgebühren, auf deren Grundlage Reisende ihre Routen anpassen. Beim Schutz kritischer Infrastrukturen müssen Schutzmechanismen so gewählt werden, dass Systeme auch in Ausnahmesituationen wie Naturkatastrophen, technischen Ausfällen oder terroristischen Angriffen funktionsfähig bleiben.
Entscheidungsprozesse, bei denen zwei verschiedene Akteure – der sogenannte Leader und der sogenannte Follower – miteinander interagieren, lassen sich mathematisch mithilfe der Bilevel-Optimierung modellieren. Dabei wird ein Optimierungsproblem in zwei Ebenen (daher die Bezeichnung „Bilevel“) unterteilt: eine führende Entscheidungsebene (Leader-Problem) und eine nachgelagerte Reaktionsebene (Follower-Problem). Ihren Ursprung hat die Bilevel-Optimierung in den Wirtschaftswissenschaften und geht auf die Arbeiten von Heinrich von Stackelberg [7,8] zurück. Im Bereich der mathematischen Optimierung wurde das Konzept erstmals von Bracken und McGill [5] formalisiert, die solche Probleme als „mathematical programs with optimization problems in the constraints“ beschrieben. Damit brachten sie bereits treffend auf den Punkt, was die Bilevel-Optimierung auszeichnet: Einige der Variablen eines Optimierungsproblems sind selbst Lösungen eines weiteren, darin eingebetteten Optimierungsproblems. Diese verschachtelte Struktur macht Bilevel-Probleme zu einem wertvollen Werkzeug für die Modellierung strategischer Entscheidungsprozesse, sie stellt aber auch erhebliche Herausforderungen dar. In [6] wurde gezeigt, dass selbst lineare Bilevel-Probleme, also solche mit kontinuierlichen Variablen, affin-linearen Zielfunktionen und affin-linearen Nebenbedingungen, im Allgemeinen stark NP-schwer sind. Zusätzliche Herausforderungen ergeben sich beispielsweise, wenn Ganzzahligkeitsaspekte, Nichtlinearitäten oder Unsicherheiten in Bilevel-Problemen berücksichtigt werden müssen.
Daten- und Entscheidungsunsicherheit in der Bilevel-Optimierung
In vielen praktischen Anwendungen müssen Entscheidungen unter Unsicherheit getroffen werden. Dies kann verschiedene Gründe haben, etwa weil Vorhersagen ungenau sind oder Problemdaten nicht exakt bestimmt werden können. Ein alltägliches Beispiel für solche Datenunsicherheiten sind schwankende Reisezeiten im Verkehrsmanagement, die infolge von Unfällen, Unwettern, Bauarbeiten oder sonstigen unerwarteten Verkehrsereignissen auftreten können.
In der Bilevel-Optimierung gibt es neben unsicheren Problemdaten allerdings noch eine weitere Quelle für Unsicherheiten. Da Bilevel-Probleme zwei verschiedene Entscheidungsträger in einem einzigen Modell berücksichtigen, können auch Unsicherheiten bezüglich der (Beobachtung der) jeweiligen Entscheidungen auftreten. Solche Entscheidungsunsicherheiten entstehen beispielsweise, wenn der Follower die Leader-Entscheidung nicht vollständig beobachten kann oder wenn der Leader eine optimale Follower-Entscheidung erwartet, dieser jedoch nur näherungsweise handelt.
Entscheidungsunsicherheiten sind spezifisch für die Bilevel-Optimierung und spielen in der einstufigen Optimierung natürlich keine Rolle, da dort nur ein einziger Entscheidungsträger betrachtet wird. Insgesamt sind die Ursachen für Unsicherheiten in der Bilevel-Optimierung somit deutlich vielfältiger als in der einstufigen Optimierung. Einen systematischen Überblick über das noch recht junge, aber sehr aktive Forschungsfeld der Bilevel-Optimierung unter Unsicherheit bietet der kürzlich erschiene Übersichtsartikel in [2].
Zur Behandlung von Unsicherheiten haben sich in der einstufigen Optimierung vor allem zwei Ansätze etabliert: stochastische und robuste Optimierung. Diese beiden Ansätze werden auch in der Bilevel-Optimierung zur Behandlung von Daten- und Entscheidungsunsicherheiten verfolgt. Während stochastische Methoden in diesem Kontext dominant sind, befindet sich die robuste Bilevel-Optimierung jedoch noch in den Kinderschuhen.
Modellierungs- und Lösungsstrategien für robuste Bilevel-Probleme
In der kumulativen Dissertation „Mixed-Integer Optimization Techniques for Robust Bilevel Problems with Here-and-Now Followers“ [1] werden verschiedene Arten von Unsicherheiten in der Bilevel-Optimierung untersucht und Möglichkeiten aufgezeigt, wie sich diese mit Techniken der robusten Optimierung behandeln lassen. Im Fokus stehen dabei Modelle mit sogenannten „here-and-now“-Followern. Bei diesen müssen sowohl der Leader als auch der Follower vor der Realisierung der Unsicherheiten, also „here-and-now“, ihre Entscheidungen treffen. Das Ziel der Arbeit ist insbesondere die Entwicklung von algorithmischen Methoden zur Lösung solcher robuster Bilevel-Probleme.
Ein besonderer Schwerpunkt der Dissertation liegt auf gemischt-ganzzahligen linearen Bilevel-Problemen unter Datenunsicherheiten, wie sie insbesondere im Kontext des Schutzes kritischer Infrastrukturen auftreten. Es werden zwei exakte Schnittebenenverfahren („branch-and-cut“) [3] sowie heuristische Lösungsansätze [4] für diese Klasse robuster Bilevel-Probleme entwickelt. Die vorgestellten Methoden sind die ersten, die diese Problemklasse direkt adressieren, und ihre Effektivität wird durch umfangreiche numerische Experimente belegt.
Neben der Datenunsicherheit werden in der Dissertation außerdem zwei Aspekte der Entscheidungsunsicherheit behandelt. Zunächst wird ein robuster Modellierungsansatz vorgestellt, in dem sich der Follower gegen fehlerhafte Wahrnehmungen der Leader-Entscheidung absichert. Anschließend wird anhand eines illustrativen Beispiels gezeigt, dass algorithmische Notwendigkeiten, die zu geringfügigen Abweichungen von einer antizipierten Follower-Entscheidung führen, schwerwiegende Folgen bei der rechnerischen Lösung von Bilevel-Problemen haben können. Diese Ergebnisse unterstreichen, dass große Sorgfalt bei der Entwicklung von Lösungsalgorithmen für Bilevel-Probleme unerlässlich ist.
Ein weiteres zentrales Thema der Dissertation ist die Optimierung von Mautgebühren in Verkehrsnetzen unter Unsicherheit.
Optimierung von Mautgebühren in Verkehrsnetzen unter Unsicherheit
In Verkehrsnetzen ist die Erhebung von Mautgebühren ein wirksames Mittel, um das Verkehrsverhalten gezielt zu steuern. Mautgebühren können dazu beitragen, Staus zu verringern und eine effizientere Nutzung der Straßenkapazitäten zu fördern. Darüber hinaus können die Einnahmen aus Mautgebühren beispielsweise für die Instandhaltung der bestehenden Infrastruktur verwendet werden. Die Festlegung von Mautgebühren ist daher ein wesentlicher Bestandteil der Verkehrswissenschaft.
In diesem Zusammenhang legt eine Verkehrsbehörde Tarife fest und schätzt gleichzeitig ab, wie die Verkehrsteilnehmenden darauf reagieren werden. Die Nutzer des Verkehrsnetzes versuchen in der Regel, ihre Reisekosten und die Reisedauer zu minimieren – ein Verhalten, das sich mithilfe sogenannter Wardrop-Gleichgewichte [9] modellieren lässt. In der Dissertation [1] wird die Optimierung von Mautgebühren als „mathematical program with equilibrium constraints“ (MPEC) formuliert. Zusätzlich wird berücksichtigt, dass die Netzwerknutzer robuste Entscheidungen treffen, um sich gegen Schwankungen in den Reisezeiten aufgrund unerwarteter Verkehrsereignisse abzusichern. In einer Fallstudie wird untersucht, welchen Einfluss die Berücksichtigung von Unsicherheiten auf das Reiseverhalten und die Einnahmen aus Mautgebühren haben kann. Es zeigt sich, dass der Umgang der Verkehrsteilnehmenden mit Unsicherheiten das Verkehrsverhalten und damit auch die Höhe der Einnahmen aus Mautgebühren deutlich beeinflussen kann. Netzwerknutzer, die sich gegen Unsicherheiten in den Reisekosten und der Reisedauer absichern, verhalten sich entweder gleichgültig gegenüber der Unsicherheit, ändern ihre Routenwahl vollständig oder entscheiden sich für eine Zwischenlösung. Insbesondere kann das angepasste Reiseverhalten im robusten Kontext zu deutlich höheren Einnahmen durch Mautgebühren führen. Abbildung 1 veranschaulicht beispielhaft die Unterschiede in den Verkehrsflüssen zwischen dem deterministischen und dem robusten Modell.
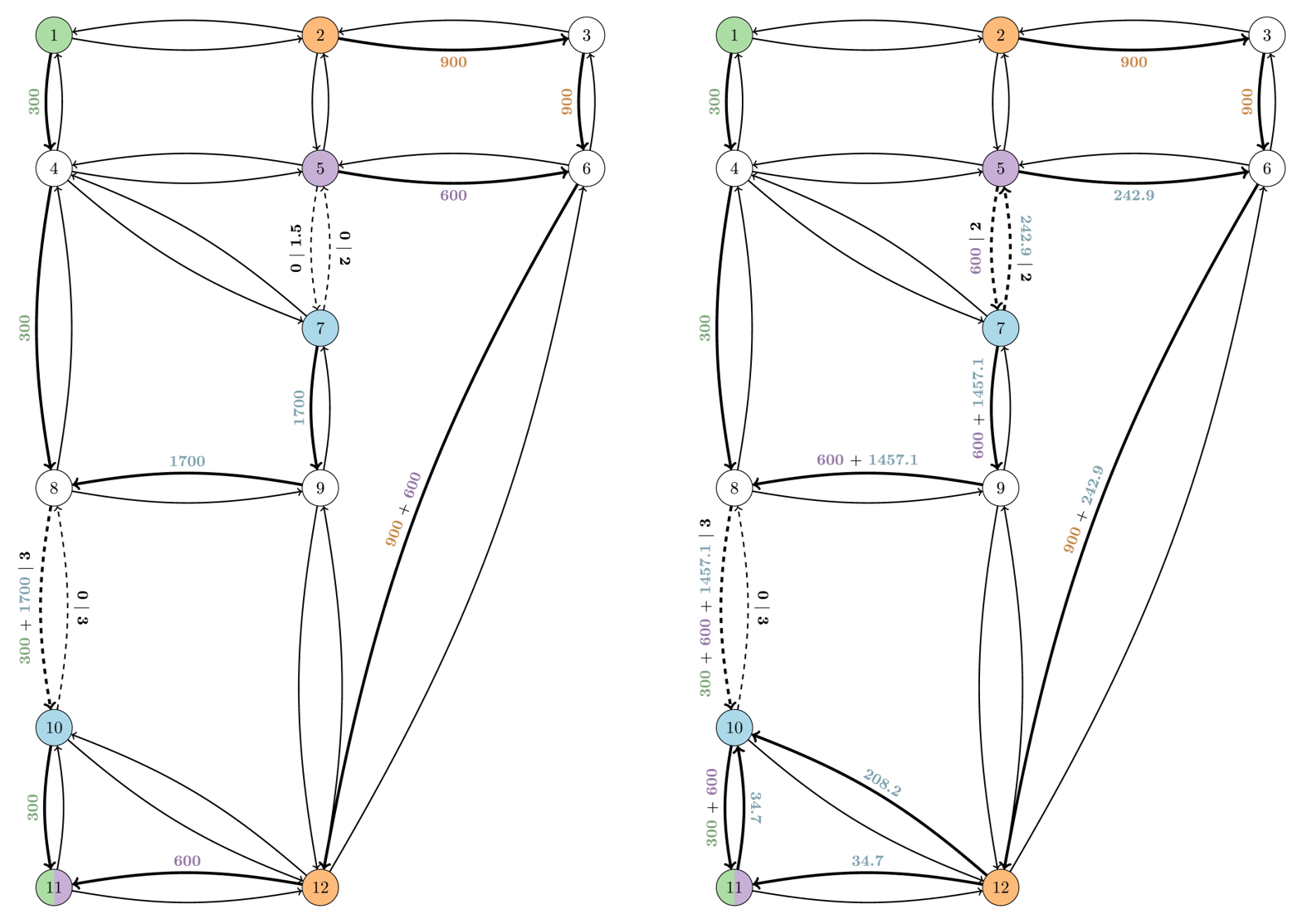
Jedes Start-Ziel-Paar ist farblich markiert (orange, grün, blau, lila). Mautpflichtige Abschnitte sind mit gestrichelten, mautfreie Abschnitte mit durchgezogenen Linien dargestellt. Die Zahlen an den Straßenabschnitten geben die Verkehrsflüsse für die jeweilige Start-Ziel-Paare an. Bei mautpflichtigen Abschnitten erfolgt die Beschriftung im Format „Fluss | Mautgebühr“. Abschnitte ohne Beschriftung werden von den Verkehrsteilnehmenden nicht genutzt. Links sind die Ergebnisse im deterministischen Modell, rechts die Ergebnisse im robusten Modell dargestellt
Fazit und Ausblick
In der Dissertation [1] werden einige der zahlreichen Herausforderungen im Kontext der Bilevel-Optimierung unter Unsicherheit adressiert. Insbesondere wird diskutiert, dass die Ursachen für Unsicherheiten in der Bilevel-Optimierung deutlich vielfältiger sind als in der klassischen, einstufigen Optimierung. In der Bilevel-Optimierung können neben den Problemdaten auch die (Beobachtung der) Entscheidungen der beteiligten Akteure unsicher sein. Sowohl für Daten- als auch für Entscheidungsunsicherheiten werden in der Arbeit Modellierungs- und Lösungsansätze entwickelt, die auf Techniken der robusten Optimierung aufbauen.
Insgesamt steckt die Forschung zur robusten Bilevel-Optimierung jedoch noch in den Kinderschuhen. Bisherige Arbeiten in diesem Feld konzentrieren sich überwiegend auf strikte oder Γ-robuste Ansätze mit Intervall- oder polyedrischen Unsicherheitsmengen. Die Berücksichtigung weiterer Geometrien von Unsicherheitsmengen sowie alternativer Robustheitskonzepte wie „light robustness“, „adjustable robustness“ oder „distributionally robust optimization“ sind interessante Richtungen für zukünftige Forschungsarbeiten.
Eine weitere Herausforderung besteht in der Entwicklung geeigneter Lösungsverfahren – sowohl exakter als auch heuristischer Natur – für gemischt-ganzzahlige (nicht-)lineare Bilevel-Probleme.
Literatur
[1] Beck, Y. Mixed-Integer Optimization Techniques for Robust Bilevel Problems with Here-and-Now Followers. PhD thesis. Trier University, Department of Mathematics, 2024. URL: https://ubt.opus.hbz-nrw.de/frontdoor/index/index/docId/2432.
[2] Beck, Y., I. Ljubić, and M. Schmidt. A survey on bilevel optimization under uncertainty. In: European Journal of Operational Research 311.2 (2023), pp. 401–426. DOI: 10.1016/j.ejor.2023.01.008.
[3] Beck, Y., I. Ljubić, and M. Schmidt. Exact methods for discrete Γ-robust interdiction problems with an application to the bilevel knapsack problem. In: Mathematical Programming Computation 15.4 (2023), pp. 733–782. DOI: 10.1007/s12532-023-00244-6.
[4] Beck, Y., I. Ljubić, and M. Schmidt. Heuristic Methods for Γ-Robust Mixed-Integer Linear Bilevel Problems. In: INFORMS Journal on Computing (2025). DOI: 10.1287/ijoc.2023.0239.
[5] Bracken, J. and J. T. McGill. Mathematical Programs with Optimization Problems in the Constraints. In: Operations Research 21.1 (1973), pp. 37–44. DOI: 10.1287/opre.21.1.37.
[6] Hansen, P., B. Jaumard, and G. Savard. New Branch-and-Bound Rules for Linear Bilevel Programming. In: SIAM Journal on Scientific and Statistical Computing 13.5 (1992), pp. 1194–1217. DOI: 10.1137/0913069.
[7] von Stackelberg, H. Marktform und Gleichgewicht. Springer, 1934.
[8] von Stackelberg, H. Theory of the market economy. Oxford University Press, 1952.
[9] Wardrop, J. G. Some Theoretical Aspects of Road Traffic Research. In: Proceedings of the Institution of Civil Engineers 1.3 (1952), pp. 325–362. DOI: 10.1680/ipeds.1952.11259.
Autorin
Yasmine Beck
ESSEC Business School
3 Av. Bernard Hirsch
95021 Cergy-Pontoise Cedex
email: yasmine.beck@essec.edu
website: https://yasminebeck.github.io/
