Autor: Charlotte Ackva
Facing the vast range of products in the e-commerce sector, more and more customers are purchasing online. To compete with the big online retailers, many local shops also offer a delivery service to their customers. However, conventional delivery by motorised vans is often inefficient due to low delivery volumes, access restrictions in city centres, and poor parking conditions.
To overcome these challenges, local shops start collaborating for joint transportation of parcels to the same region. For this, micro-hubs are used as intermediate storage and transhipment facilities. This increases consolidation opportunities in the delivery process: shops bring their goods to a close-by micro-hub. There, parcels are picked up by a shared vehicle for further transportation to other micro-hubs close to the parcels’ destinations. The shared vehicle is conducting a consistent tour, i.e. visiting the same micro-hubs at the same time every day. While this gives planning stability to storekeepers, customers, and drivers, finding an effective consistent schedule is challenging. Since customer orders vary from day to day, it highly depends on the consistent schedule which of these orders can be fulfilled. Figure 1 exemplarily shows a consistent schedule for two different demand realisations.
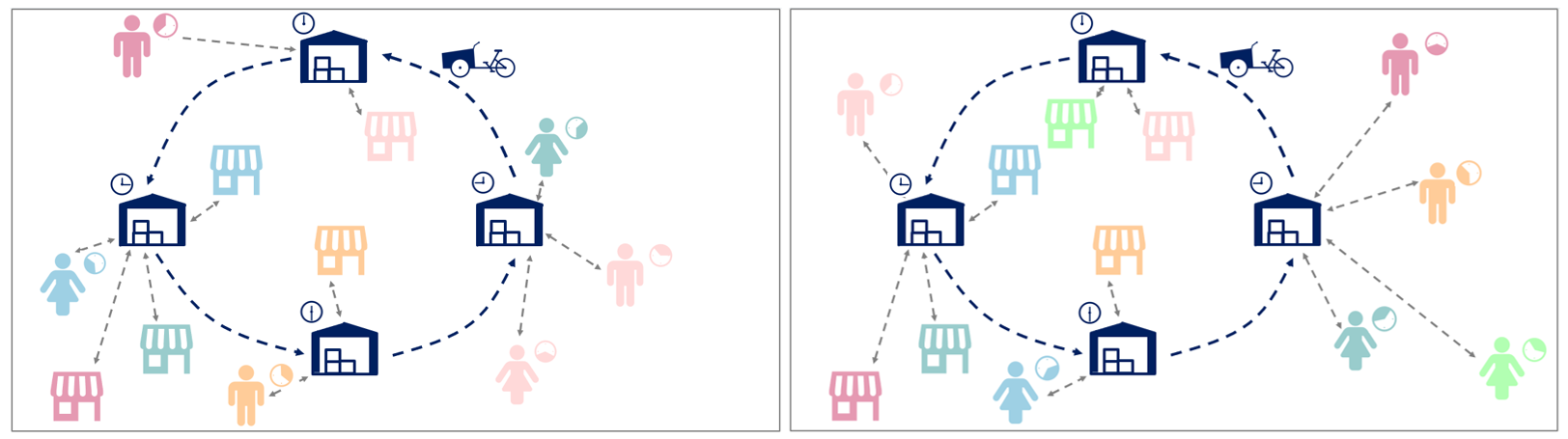
Figure 1: Example of a consistent tour for two different demand realisations (own illustration).
We formulate the problem as a two-stage stochastic optimisation model aiming to maximise the expected number of fulfilled customer orders. At the first stage, when demand is still unknown, the vehicle’s schedule is determined. At the second stage, the flow of parcels is decided based on the schedule from the first stage.
We apply the Progressive Hedging (PH) Algorithm to determine a consistent schedule. While convergence of PH is shown for convex programs, this does not hold true for integer programs anymore. Therefore, we investigate the performance of the algorithm for different parameter settings and different demand patterns. We find that PH performs rather poorly when demand is randomly distributed, but yields particularly good results when structural information of the demand distribution is available.
